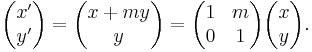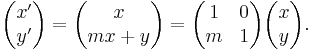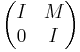Shear mapping

In mathematics, shear mapping or transvection is a particular kind of linear mapping. Linear mapping is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. A shear mapping's effect leaves all points on one axis fixed, while the other points are shifted parallel to the axis by a distance proportional to their perpendicular distance from that axis.

Shear mappings carry areas into equal areas, as they preserve the width, length, and etc. of parallelograms; see equi-areal mapping for the reason and for other linear mappings that have this property.

Elementary form

In the plane {(x, y): x,y ∈ R }, a horizontal shear (or shear parallel to the x axis) is represented by the linear mapping

\begin{pmatrix}x^\prime \\y^\prime \end{pmatrix} = \begin{pmatrix}x %2B my \\y \end{pmatrix} = \begin{pmatrix}1 & m\\0 & 1\end{pmatrix} \begin{pmatrix}x \\y \end{pmatrix}.

This leaves horizontal lines y = c invariant, but for m ≠ 0 maps vertical lines x = a into lines y' = (x'  − a)/m having slope 1/m

Substituting 1/m for m in the matrix gives lines y = m(x − a) of slope m, if desired.

A vertical shear (or shear parallel to the y axis) of lines is accomplished by the linear mapping

\begin{pmatrix}x^\prime \\y^\prime \end{pmatrix} = \begin{pmatrix}x \\ mx %2B y \end{pmatrix} = \begin{pmatrix}1 & 0\\m & 1\end{pmatrix} \begin{pmatrix}x \\y \end{pmatrix}.

The vertical shear leaves vertical lines x = a invariant, but maps horizontal lines y = b into lines y' = mx'  + b

The matrices above are special cases of shear matrices, which allow for generalization to higher dimensions. The shear elements here are either m or 1/m, case depending.

The following applications of shear mapping were noted by William Kingdon Clifford:

"A succession of shears will enable us to reduce any figure bounded by straight lines to a triangle of equal area."
"... we may shear any triangle into a right-angled triangle, and this will not alter its area. Thus the area of any triangle is half the area of the rectangle on the same base and with height equal to the perpendicular on the base from the opposite angle."

The area-preserving property of a shear mapping can be used for results involving area. For instance, the Pythagorean theorem has been illustrated with shear mapping (see external link).

Advanced form

For a vector space V and subspace W, a shear fixing W translates all vectors parallel to W.

To be more precise, if V is the direct sum of W and W′, and we write vectors as

v = w + w′

correspondingly, the typical shear fixing W is L where

L(v) = (w + Mw′) + w ′

where M is a linear mapping from W′ into W. Therefore in block matrix terms L can be represented as

\begin{pmatrix} I & M \\ 0 & I \end{pmatrix}

with blocks on the diagonal I (identity matrix), with M above the diagonal, and 0 below.

References